基础
一、 堆就是用数组实现的二叉树
堆常用方法:
- 构建优先队列
- 支持堆排序
- 快速找出集合中的最小值(或最大值)
分为:最大堆和最小堆,两者差异在于节点的排序方式,在最大堆中,父节点的值比每一个子节点的值都要大。在最小堆中,父节点的值比每一个子节点的值都要小。
二、 目的
将最大(最小)的节点放在最前面,从而进行快速的插入、删除等操作。在二叉树中搜索会很快,但是在堆中搜索会很慢。
注意:堆的根节点中存放的是最大或者最小元素,但是其他节点的排序顺序是未知的。例如,在一个最大堆中,最大的那一个元素总是位于 index 0 的位置,但是最小的元素则未必是最后一个元素。唯一能够保证的是最小的元素是一个叶节点,但是不确定是哪一个。
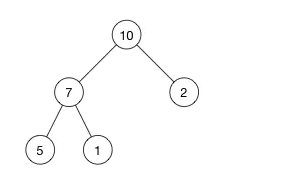
parent(i) = Math.floor((i - 1)/2)
left(i) = 2i + 1
right(i) = left + 1
| Node | Array index (i) | Parent index | Left child index | Right child index |
|---|---|---|---|---|
| 10 | 0 | -1 | 1 | 2 |
| 7 | 1 | 0 | 3 | 4 |
| 2 | 2 | 0 | 5 | 6 |
| 5 | 3 | 1 | 7 | 8 |
| 1 | 4 | 1 | 9 | 10 |
具体ts实现:
class MyHeap {
myHeap: number[]
flag: number
size: number
constructor(arr: number[] = [], type: string = 'MAX') {
this.flag = type === 'MAX' ? 1 : -1
this.myHeap = arr
this.size = arr.length
this.heapfiy()
}
/**
* @description 堆化
*/
heapfiy (): void {
this.myHeap.unshift(null)
const lastParentIndex = Math.floor(this.size / 2)
for (let i = lastParentIndex; i > 0; i--) {
this.shiftDown(this.myHeap, i, this.size)
}
this.myHeap.shift()
}
/**
* @param arr 待检查数组
* @param i 检查的起始下标
* @param s 堆大小
* @description 向下
*/
shiftDown (arr: number[], i: number, s?: number): void {
let size = s ? s : this.size
let left = 2 * i
let right = left + 1
// 左右孩子中较大/较小的那一个
let theFitOne = 0
//无左右孩子节点
if (left > size && right > size) {
return
}
//只有左孩子节点
if (left <= size && right > size) {
theFitOne = left
}
//只有右孩子节点
if (right <= size && left > size) {
theFitOne = right
}
//同时有左右孩子节点
if (left <= size && right <= size) {
theFitOne = arr[left] * this.flag < arr[right] * this.flag ? right : left
}
if (arr[i] * this.flag < arr[theFitOne] * this.flag) {
this.swap(arr, i, theFitOne)
this.shiftDown(arr, theFitOne, size)
}
}
/**
* @param i 需要移动的元素节点索引
* @description 将当前节点元素层层向上交换位置
*/
shiftUp (arr: number[], i: number): void {
const parent = Math.floor((i - 1) / 2)
if (arr[i] * this.flag < arr[parent] * this.flag || parent <= 0) {
return
} else {
this.swap(arr, i, parent)
this.shiftUp(arr, parent)
}
}
swap (arr: number[], i: number, j: number): void {
let temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
/**
* @param el 插入的元素
* @description 返回插入好的堆
*/
insert (el: number): number[] {
this.myHeap.push(el)
const i = this.myHeap.length - 1
this.shiftUp(this.myHeap, i)
this.size++
return this.myHeap
}
/**
* @description 弹出最值
*/
pop (): number {
const { myHeap } = this
// 交换第一个和最后一个元素
this.swap(myHeap, 0, myHeap.length - 1)
myHeap.unshift(null)
const top = myHeap.pop()
this.shiftDown(myHeap, 1, myHeap.length - 1)
myHeap.shift()
this.size--
return top
}
/**
* @description 返回堆排序好的新数组,不影响原数组
*/
sort (): number[] {
const { myHeap } = this
const arr = [...myHeap]
arr.unshift(null)
for (let j = arr.length - 1; j > 1; j--) {
this.swap(arr, 1, j)
this.shiftDown(arr, 1, j - 1)
}
arr.shift()
return arr
}
/**
* @description 用删除节点就返回最大值(最大堆)或者最小值(最小堆)
*/
peek (): number {
return this.myHeap[0]
}
/**
* @param i 被替换元素的坐标
* @param el 替换的内容
* @description 替换指定位置的元素
*/
replace (i: number, el: number): void {
const { myHeap } = this
let orgin = myHeap[i]
myHeap.unshift(null)
i = i + 1
myHeap.splice(i, 1, el)
if ((el > orgin && this.flag > 0) || (el < orgin && this.flag < 0)) {
this.shiftUp(myHeap, i)
} else {
this.shiftDown(myHeap, i)
}
myHeap.shift()
}
}
测试:
var arr = [7,5,8,4,9,3,2,6,2]
console.log(arr)
var minHeap = new MyHeap([...arr], 'MIN')
minHeap.peek()
leetCode
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出两块 最重的 石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下,就返回 0。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/last-stone-weight\
```js
function lastStoneWeight(stones) {
const sts = new MyHeap(stones, “MAX”);
while (sts.myHeap.length > 1) {
const one = sts.pop();
const two = sts.peek();
const diff = one - two;
if (diff > 0) {
sts.replace(0, diff);
} else {
sts.pop();
}
}
return sts.myHeap[0] || 0;
}
执行用时:96 ms, 在所有 TypeScript 提交中击败了32.08%的用户
内存消耗:40.5 MB, 在所有 TypeScript 提交中击败了24.53%的用户
= =! 还不如我之前两次提交呢
### 参考资料:
- [数据结构:堆(Heap)](https://www.jianshu.com/p/6b526aa481b1)
- [JS数据结构与算法之《堆》](https://zhuanlan.zhihu.com/p/144699737?utm_source=wechat_session&utm_medium=social&utm_oi=559769045767880704)
