类型
- 二叉树(Binary Tree):每个节点最多含有两个子节点。
- 满二叉树(Full Binary Tree):在满二叉树中,每个不是尾结点的节点都有两个子节点
- 完全二叉树(Complete Binary Tree):假设一个二叉树的深度(depth) 为d(d>1),除了第d层外,其他各层的节点数量均已达到最大值,且第d层所有节点从左向右紧密排列,这样的二叉树就是完全二叉树。
- 排序二叉树(Binary Search Tree):在此树中,每个节点的数值比左子树的每个节点都大,比所有右子树上的节点都小。
- 平衡二叉树(AVL Tree):任何节点的两颗子树的高度差不大于1的排序二叉树。
- B树(B-Tree):B树和平衡二叉树一样,只不过它是一种多叉树(一个节点的子节点数量可以超过二)
- 红黑树(Red-Black Tree):是一种自平衡二叉寻找树
排序二叉树实现
class TreeNode {
val: number
left: TreeNode | null
right: TreeNode | null
constructor(val: number) {
this.val = val
this.left = this.right = null
}
show () {
return this.val
}
}
class BST {
root: null | TreeNode
constructor() {
this.root = null
}
insert (val: number): void {
if (!val) {
return
}
const node = new TreeNode(val)
if (!this.root) {
this.root = node
return
}
let current = this.root
let parent = null
while (current) {
parent = current
if (val < current.val) {
current = current.left
if (!current) {
parent.left = node
}
} else {
current = current.right
if (!current) {
parent.right = node
}
}
}
}
remove (val: number): boolean {
if (!val) {
return false
}
let { root } = this
let current = root
let parent = null
let isLeftChild = false
while (current && current.val !== val) {
parent = current
if (val < current.val) {
current = current.left
isLeftChild = true
} else {
current = current.right
isLeftChild = false
}
}
if (!current) {
return false
}
// 1.删除的元素没有子元素
if (!current.left && !current.right) {
if (current === root) {
root = null
} else {
isLeftChild ? (parent.left = null) : (parent.right = null)
}
}
// 2.删除的元素只有一个子元素
else if (!current.left) {
if (current === root) {
root = current.right
} else {
isLeftChild ? (parent.left = current.right) : (parent.right = current.right)
}
} else if (!current.right) {
if (current === root) {
root = current.left
} else {
isLeftChild ? (parent.left = current.left) : (parent.right = current.left)
}
}
// 3. 被删除的元素有两个子元素
else {
const successor = this.getSuccessor(current)
if (current === root) {
root = successor
} else {
isLeftChild ? (parent.left = successor) : (parent.right = successor)
}
// 将被删除的元素的右边赋值给新节点的右边
successor.right = current.right
}
return true
}
/**
*
* @param node 被删除的元素
* @description 返回被删除元素左边最大的子元素
*/
private getSuccessor (node: TreeNode): TreeNode {
let successor = null
let successorPerent = null
let current = node.left
while (current) {
successorPerent = successor
successor = current
current = current.right
}
if (successor !== node.left) {
successorPerent.right = successor.left
successor.left = node.left
}
return successor
}
search (val: number): TreeNode | null {
if (!val) {
return null
}
let current = this.root
let parent = null
while (current && current.val !== val) {
parent = current
if (val < current.val) {
current = current.left
} else if (val > current.val) {
current = current.right
}
}
return current ? current : null
}
/**
*
* @param node
* @param arr
* @description 自己 -> 左 -> 右
*/
preOrder (node?: TreeNode, arr?: number[]): number[] {
if (!node && !arr) {
node = this.root
}
arr = arr ? arr : []
if (node) {
arr.push(node.val)
this.preOrder(node.left, arr)
this.preOrder(node.right, arr)
return arr
}
}
/**
*
* @param node
* @param arr
* @description 左 -> 自己 -> 右
*/
inOrder (node?: TreeNode, arr?: number[]): number[] {
if (!node && !arr) {
node = this.root
}
arr = arr ? arr : []
if (node) {
this.inOrder(node.left, arr)
arr.push(node.val)
this.inOrder(node.right, arr)
return arr
}
}
/**
*
* @param node
* @param arr
* @description 左 -> 右 -> 自己
*/
postOrder (node?: TreeNode, arr?: number[]): number[] {
if (!node && !arr) {
node = this.root
}
arr = arr ? arr : []
if (node) {
this.postOrder(node.left, arr)
this.postOrder(node.right, arr)
arr.push(node.val)
return arr
}
}
/**
*
* @param node 查找的节点
* @param deep 累加的层数
* @description 查找当前树的层级,不传参表示从根节点开始数
*/
getDeep (node?: TreeNode, deep?: number): number {
if (!node && !deep) {
node = this.root
}
deep = deep || 0
if (!node) {
return deep
}
deep++;
let deepLeft = this.getDeep(node.left, deep)
let deepRight = this.getDeep(node.right, deep)
return Math.max(deepLeft, deepRight)
}
getMin (): number {
let current = this.root
while (current) {
if (!current.left) {
return current.val
}
current = current.left
}
}
getMax (): number {
let current = this.root
while (current) {
if (!current.right) {
return current.val
}
current = current.right
}
}
}
遍历
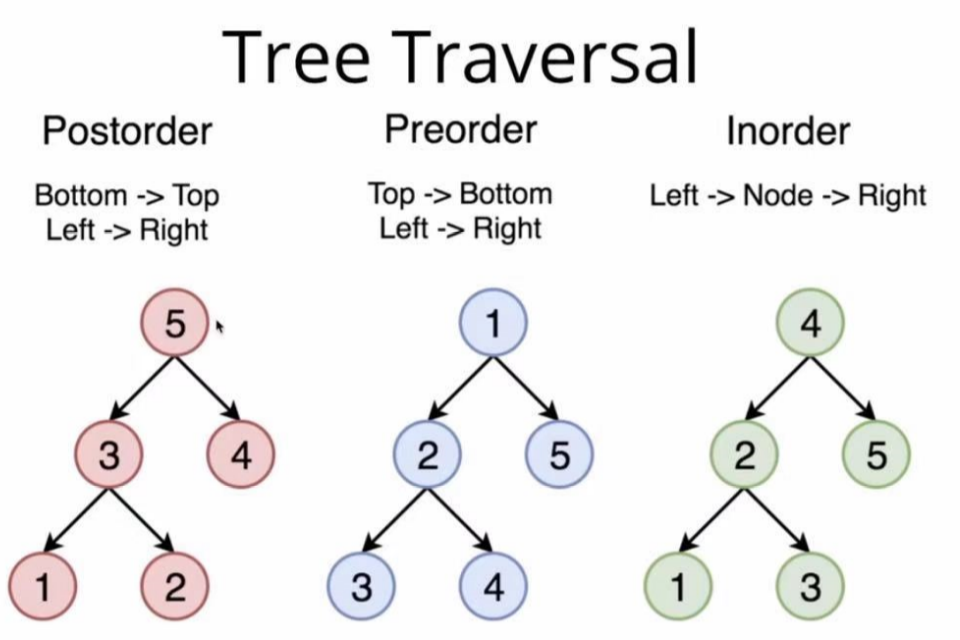
- Pre-order Traveral:先访问节点自己,然后访问左子树,最后再访问右子树
- In-order Traveral: 先访问左子树上的节点,再访问自己,最后再访问右子树的节点, 结合排序二叉树 可以从小到大排序
- Post-order Traveral: 先访问左右子树,最后访问自己
测试一下
var bst = new BST()
bst.insert(8)
bst.insert(1)
bst.insert(3)
bst.insert(2)
bst.insert(14)
bst.insert(11)
bst.insert(9)
bst.insert(10)
bst.insert(13)
bst.insert(12)
bst.insert(18)
bst.inOrder() // [1, 2, 3, 8, 9, 10, 11, 12, 13, 14, 18]
bst.preOrder() // [8, 1, 3, 2, 14, 11, 9, 10, 13, 12, 18]
bst.postOrder() // [2, 3, 1, 10, 9, 12, 13, 11, 18, 14, 8]
参考资料

